Problem Solving with Sequential Programs
Problems
While every science focuses on solving problems from its domain, in computer science the focus is on problem solving in general. Computers are tools used in all disciplines to help solve the problems of that discipline. For this reason we call computers general purpose problem solvers.Computers, and the programs that run on them, are not without their own restrictions. We might intend them to help us solve any problem, but at the present moment they are restricted by the advancement of our technology. Since most computers are still trapped inside a box (no arms/legs/eyes let alone autonomy) they are restricted in the types of problems they can help solve. We call problems that can be solved by a computer computational problems.
Computers are specialized for computing, specifically the task of processing information. The computer receives the initial information as input and then processes the information, possibly altering it or computing new information, and then displays or returns final information as output.Input could consist of a whole file of data, a selection made with a mouse click, a collection of keystrokes, or just a single keystroke. Output can range from files of calculated data, video and audio output to the screen and speakers, turning on/off components, or in some cases nothing at all. In rare cases our modern computers are equipped with limbs or a means of locomotion and we call these computers robots. Other than robots, computers have very limited power to manipulate the physical world, but have enormous power in the world of information. A computational problem is one where the solution involves merely information processing.
Computational Problems
Let’s consider some real world problems we might encounter and try to determine which parts are computational – having to do with information processing – and which parts are physical – requiring physical labour of some kind.
Calculating a Sum
Imagine we have a list of ten numbers and we need to add them up. This problem is already purely computational. If we have a convenient way to enter the numbers into the computer (say a spreadsheet) we can easily get the computer to do the information processing of adding the numbers together.
Arithmetic problems and other math problems were the ideal problems for computers to solve and the first computers were put to specialized uses like calculators. We use these formal math problems as a model for how to find other computational problems in real world problems.
Travelling to a New Destination
Often in life we must get ourselves to someplace we have never been before. Our goal here is to separate the computational task from the physical task. In travelling to a new place we must know how to get there and then travel along the selected path. Finding the path or selecting the path is a largely computational problem, given some reasonable input like a map or a list of bus routes, flight plans, etc. In fact Google Maps is a technology that solves this computational problem for you. You tell it where you begin, where you would like to end up, and how you would like to travel (by foot, car, train, etc) and it will select a path for you.However, Google Maps cannot do all the work for you. Once you have the route selected it is still up to you to physically follow the route. This means that you can still fail to solve the problem physically even if you have successfully solved the problem computationally.
Erecting a Building
Say we plan to build a new building, maybe a house or skyscraper. Again we wish to focus on the computational aspects of the task. Designing the building, before the foundation has been laid, is a largely computational problem. Programs like AutoCAD allow a designer to manipulate the blueprints of the structure without having to erect the physical building. However, once designed the house must still be physically erected by many skilled workers.Further, once the building is under construction the building team may encounter new problems like where to add ductwork, wiring, plumbing, etc to the plan that might not have included all details. This may require going “back to the drawing board” as it were, or in our case back to the computer to deal with more computational aspects of the problem. It is common in the real world to have to swap back and forth between the computational and physical aspects of a problem.
Digging a Hole
Say we need to dig a post hole. As much as I would love to turn this problem into a computational one it just isn’t. You can spend as much time as you like planning the dig, the angle to use the shovel, etc, but it won’t help you as the problem is almost purely physical. Some problems are just this way, and this is the limit of computation (today).Remember there are computers with arms and legs today, and one day they will be able to dig holes for us too.
Programs
Now that we have some idea what a computational problem is – some informational input we want to process into some informational output – we can focus on solving the problem. A computational problem solution in the real world is called a program. A program runs on a computer and is a specific problem solver. That is, it solves one problem or possibly a collection of closely related problems as opposed to solving many different problems.A program in the sequential programming paradigm is a sequence of steps or operations. Carrying out the steps in sequence is called running the program and if the program is correct this will solve the computational problem. We call this paradigm the sequential programming paradigm because the steps must be processed in sequence. This is in contrast to the parallel programming paradigm where many operations may be carried out at the same time. We will discuss this paradigm in more detail at a later stage.
Each step or operation in the program is going to be a simple behavior or action the computer can do at once. What these operations are depends usually on the type of problem you are solving and the programming language that you are using. We will look at programming languages as well but for now we will attempt to be language independent. To do this we will consider a fairly simple navigation problem to get us started.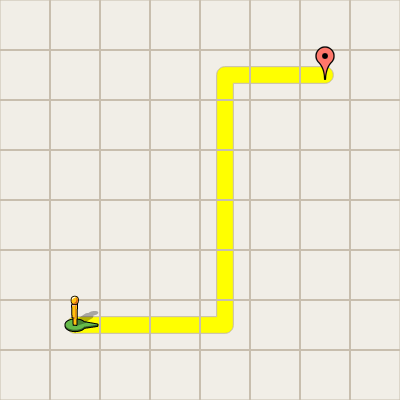
Straight Line Programs
Blocky is a simple programming aide designed at Google that allows for us to program easily without making a lot of errors. We will begin by using Blocky as a tool to understand simple programming concepts. To help us understand sequential programs better we can play with this simple demo.This demo consists of a figure in a simple maze. The commands we can give the figure are simple. The figure can move forward, turn left 90 degrees, and turn right 90 degrees. We wish to get the figure to its destination by giving it a correct set of instructions.
Notice that more than one correct program can exist for this problem. We can see this by noting that we can take a sequence of actions that returns us to where we started. If you turn left 90 degrees four times you will end up facing the same direction. Or if you step forward, turn left 90 degrees twice, step forward and turn left 90 degrees twice you will again be in the same position and orientation as before. Due to these loops we can see that there are actually infinite correct programs for this one maze.
Correctness is not the only important feature of a program. Among the correct solutions we usually prefer the ones that solve the problem with fewer operations. We call these the more efficient solutions. Correctness and efficiency are the two main measures of a program’s value.